Clustering in the HCS
The HCS is the simplest non-trivial particulate gas-solid system. The continuum gas-phase is initially at rest. The particles are uniformily distributed in space and have zero momentum in all three directions. However, the particle pecular velocity is non-zero, quantified by an initial granular temperature, \(T_0\). The system is periodic in all directions and no external forces act on the system. Under homogeneous conditions, the granular temperature, \(T\), is equivalent to two-thirds of the the (massless) mean particle kinetic energy. In the HCS, the Eulerian kinetic theory (KT) model of Garzo et al. [GTSH12] reduces to:
where \(m\) is the particle mass, \(\gamma\) is the thermal drag and \(\zeta_0\) is the zeroth-order cooling rate. The first term on the RHS above represents viscous dissipation due to the interstitial gas while the second term represents collisional dissipation due inelastic particle-particle interactions. The ODE has an analytical solution given by Yin et al. [YZMH13] (also see [LBFHHGS16] for the exact model used herein which also includes a first-order thermal Reynolds number extension to \(\gamma\)). In the absence of clustering, the granular temperature in the HCS decays according to the analytical solution, known as Haff’s law [H83] in granular systems: \(\gamma = 0\). However, at a critical system size [G05], \(L^*_c\), (where \(L^* = L/d_p\)), the initially homogeneous state gives way to the most fundamental of gas-solid instabilities, the clustering instability, which causes \(T\) (or more accurately \(KE\)) to deviate significantly from KT solution due to regions of high and low concentration and correlated motion.
To test if MFIX-Exa predicts the expected clustering behavior, a system is set up with the following non-dimensional parameters:
initial thermal Reynolds number: \(Re_{T_0} = \rho_g d_p \sqrt{T_0} / \mu_g = 20\)
density ratio: \(\rho^* = \rho_p / \rho_g = 1000\)
restitution coefficient: \(e = 0.8\)
solids concentration: \(\phi = \pi N_p / 6 L^*_x L^*_y L^*_z \approx 0.05\)
While not specifically studied by Fullmer et al. [FLYH18], their results
indicate that \(L_c^*\) may be as large as 100 at these conditions.
In order to avoid the region near critical stability, we use a significnatly
larger system size: \(L^*_x = L^*_y = 256\). The system is thin in the
depth dimension, \(L^*_z = 8\) in order to highlight the clustering
phenomena. Therefore, \(N_p = 50000\). Because the system is hypothetical,
the ideal BVK2 DNS drag law is applied, see [BvK07], [TPKKv15].
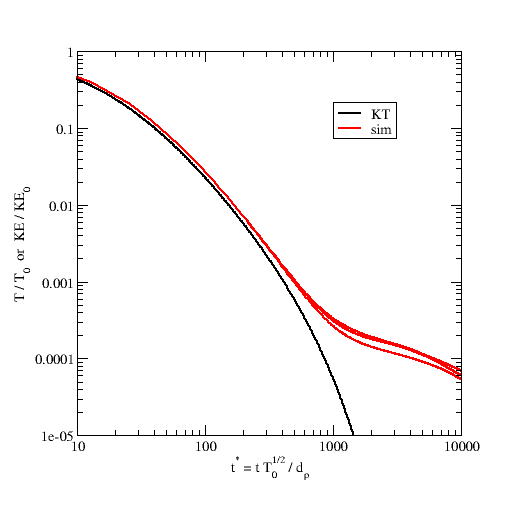
Fig. 5 Decay of the particle mean kinetic energy compared to the KT analytical soluiton of the GTSH model.
Three replicate systems are simulated with MFIX-Exa 19.08, differing only in initial particle locations and pecular velocities. The particle kinetic energy is averaged in the simulations (red) and compared to the analytical granular temperature (black) of the HCS as a function of time in the figure above. The kinetic energy \(KE / KE_0\) decays by two to three orders of magnitude in line with the HCS result until clustering and localized mean motion cause a drastic deviation. The final result at \(t^* = 1000\) for one of the replicates is shown below (at right) compared to the seminal result of Goldhirsch and Zanetti [GZ93] (true 2D), the original demonstration of the clustering instability the HCS.
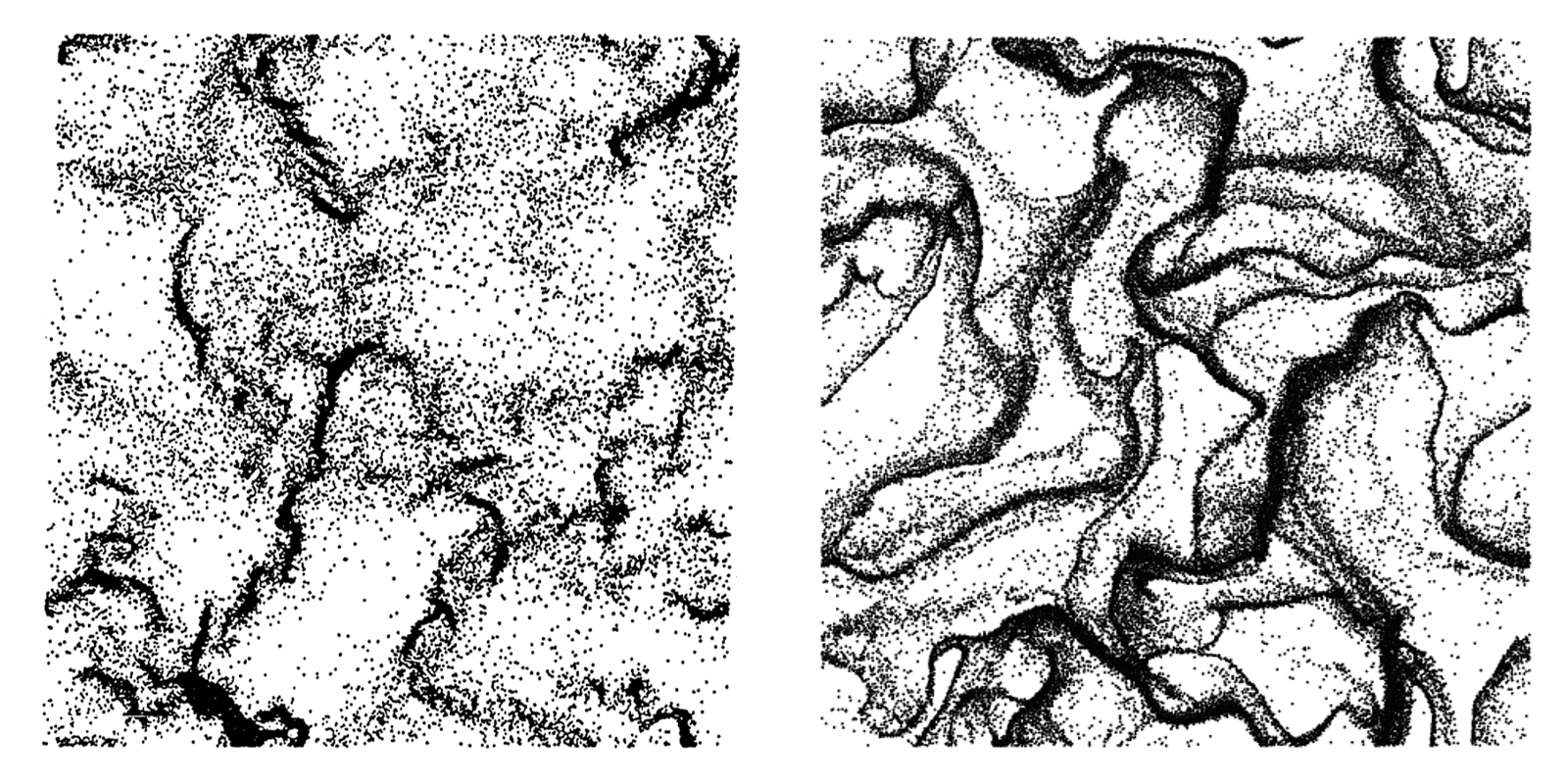
Fig. 6 Clustered state of the HCS observed by Goldhirsch and Zanetti [GZ93] (left) compared to an MFIX-Exa result (right).